- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 6. Simulation Methods
- Subject 3. Bootstrapping
Why should I choose AnalystNotes?
Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.
Subject 3. Bootstrapping PDF Download
Resampling is a way to reuse data to generate new, hypothetical samples (called resamples) that are representative of an underlying population. Resampling is used when:
- You don't know the underlying distribution for the population,
- Traditional formulas are difficult or impossible to apply,
- As a substitute for traditional methods.
The bootstrap method is a resampling technique used to estimate statistics on a population by sampling a dataset with replacement.
Both bootstrapping and traditional methods use samples to draw inferences about populations. Both can estimate sampling distributions. A primary difference is how they estimate sampling distributions.
Traditional methods use properties of the sample data, the experimental design, a test statistic and need to satisfy the assumptions.
The bootstrap method involves iteratively resampling a dataset with replacement. This method takes the sample data that a study obtains, and then resamples it over and over to create many simulated samples. Each of these simulated samples has its own properties, such as the mean. When you graph the distribution of these means on a histogram, you can observe the sampling distribution of the mean. You don't need to worry about test statistics, formulas, and assumptions.
Example
Suppose a study collects five data points and creates four bootstrap samples:
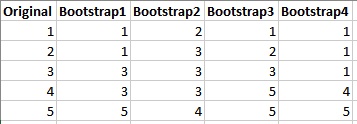
The resampled datasets are the same size as the original dataset and only contain values that exist in the original set. Furthermore, these values can appear more or less frequently in the resampled datasets than in the original dataset. Finally, the resampling process is random and could have created a different set of simulated datasets.
keep in mind that bootstrapping does not create new data. Instead, it treats the original sample as a proxy for the real population and then draws random samples from it. Consequently, the central assumption for bootstrapping is that the original sample accurately represents the actual population. As the sample size increases, bootstrapping converges on the correct sampling distribution under most conditions.
User Contributed Comments 0
You need to log in first to add your comment.

I am using your study notes and I know of at least 5 other friends of mine who used it and passed the exam last Dec. Keep up your great work!

Barnes
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add