- CFA Exams
- 2026 Level I
- Topic 3. Corporate Issuers
- Learning Module 5. Capital Investments and Capital Allocation
- Subject 2. Capital Allocation
Seeing is believing!
Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.
Subject 2. Capital Allocation PDF Download
The capital allocation process is the process of planning expenditures on assets (fixed assets) whose cash flows are expected to extend beyond one year. Managers analyze projects and decide which ones to include in the capital budget.
- "Capital" refers to long-term assets.
- The "budget" is a plan which details projected cash inflows and outflows during a future period.
Steps in the Capital Allocation Process
The typical steps:
- Idea Generation. Generating good investment ideas to consider.
- Investment Analysis. Analyzing individual proposals (forecasting cash flows, evaluating profitability, etc.).
- Capital Allocation Planning. How does the project fit within the company's overall strategies? What's the timeline and priority?
- Monitoring and Post-Auditing. It is a follow-up of capital allocation process and a key element. By comparing actual results with predicted results and then determining why differences occurred, decision-makers can improve forecasts (based on which good capital allocation decisions can be made). Otherwise, you will have the GIGO (garbage in, garbage out) problem. Improve operations, thus making capital decisions well-implemented.
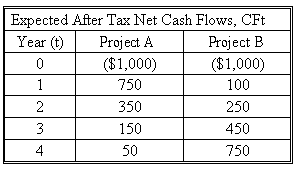
When a firm is embarking upon a project, it needs tools to assist in making the decision of whether to invest in the project or not. In order to demonstrate the use of these two methods, the cash flows presented below will be used.
Net Present Value (NPV)
This method discounts all cash flows (including both inflows and outflows) at the project's cost of capital and then sums those cash flows. The project is accepted if the NPV is positive.
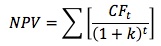
where CFt is the expected cash flow at period t, k is the project's cost of capital, and n is its life.
- Cash outflows are treated as negative cash flows since they represent expenditures of the company to fund the project.
- Cash inflows are treated as positive cash flows since they represent money being brought into the company.
The NPV represents the amount of present-value cash flows that a project can generate after repaying the invested capital (project cost) and the required rate of return on that capital. An NPV of zero signifies that the project's cash flows are just sufficient to repay the invested capital and to provide the required rate of return on that capital. If a firm takes on a project with a positive NPV, the position of the stockholders is improved.
Decision rules:
- The higher the NPV, the better.
- Reject if NPV is less than or equal to 0.
NPV measures the dollar benefit of the project to shareholders. However, it does not measure the rate of return of the project, and thus cannot provide "safety margin" information. Safety margin refers to how much the project return could fall in percentage terms before the invested capital is at risk.
Assuming the cost of capital for the firm is 10%, calculate each cash flow by dividing the cash flow by (1 + k)t where k is the cost of capital and t is the year number. Calculate the NPV for Project A and B above.
NPV = CF0 + CF1 + CF2 + CF3 + CF4
Project A's NPV = -1,000 + 750/1.101 + 350/1.102 + 150/1.103 + 50/1.104 = -1,000 + 682 + 289 + 113 + 34 = $118 (rounded)
Project B's NPV = -1,000 + 100/1.101 + 250/1.102 + 450/1.103 + 750/1.104 = -1,000 + 91 + 207 + 338 + 512 = $148 (rounded)
Internal Rate of Return (IRR)
This is the discount rate that forces a project's NPV to equal zero.
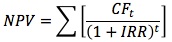
Note that this formula is simply the NPV formula solved for the particular discount rate that forces the NPV to equal zero. The IRR on a project is its expected rate of return. The NPV and IRR methods will usually lead to the same accept or reject decisions.
Decision rules:
- The higher the IRR, the better.
- Define the hurdle rate, which typically is the cost of capital.
- Reject if IRR is less than or equal to the hurdle rate.
IRR does provide "safety margin" information.
Calculate Project A's and B's IRR.
Project A: -1000 + 750/(1 + IRR)1 + 350/(1+IRR)2 + 150/(1+IRR)3 + 50/(1+IRR)4 = 0
Since it is difficult to determine by hand, the use of a financial calculator is needed to solve for IRR.
The IRR for Project A is 18.32% and for Project B is 15.03%.
Return on Invested Capital
Return on invested capital (ROIC) measures a company's profitability relative to the amount of total invested capital.
ROIC reflects the effectiveness of a company's management in converting capital into profits, regardless of what type of capital is used (e.g., debt, equity).
Note:
- Working capital is not included.
- Interest expense is not subtracted from the after-tax operating profit. This is because the cost that the company incurs to finance its debt represents a return to its lenders.
- Data is easily-accessible to calculate ROIC.
- It can be broken into 2 components: ROIC = [after-tax operating profit / Sales] x [Sales / Average invested capital] = after-tax operating profitability x asset turnover
- ROIC allows outside analysts to assess a company's value-creation ability at an aggregate level rather than at the level of individual projects.
- Investors can compare ROIC to the rate of return that they require as compensation. Companies create value for investors by generating an ROIC in excess of their cost of capital.
- It is accounting-based, not cash-based (like NPV and IRR). Numbers can be manipulated with choices regarding depreciation, capital expenditures, and recognition of revenues and expenses. Further adjustments are needed on items such as pension obligations, deferred tax liabilities, and leases.
- It is a backward-looking measure that can be highly volatile, which makes it difficult for analysts to identify trend rates.
- It is an aggregate measure that can mask differences in profitability among various capital projects.
- The IRR is the discount rate that sets the NPV to 0.
- The NPV profile declines as the discount rate increases.
- Project A has a higher NPV at low discount rates, while Project B has a higher NPV at high discount rates. The NPV profiles of Project A and B join at the crossover rate, at which the projects' NPVs are equal.
- The slope of Project A's NPV profile is steeper. This indicates that Project A's NPV is more sensitive to changes in the discount rates.
- The IRR criterion for accepting an independent project is IRR > hurdle rate. That is, the cost of capital must be less than (or to the left of) the IRR.
- Whenever the cost of capital is less than the IRR, the project's NPV is positive. Recall the decision rule for independent projects: accept if NPV > 0. Thus, both projects should be accepted based on the NPV method.
- If the cost of capital > crossover rate, then NPVB > NPVA and IRRB > IRRA. Thus, both methods lead to the selection of Project B.
- If the cost of capital < crossover rate, then NPVB < NPVA and IRRB > IRRA. Thus, a conflict arises because now the NPV method will select Project A while the IRR method will choose B.
- Therefore, for mutually exclusive projects, the NPV and IRR methods lead to same decisions if the cost of capital > the crossover rate and different decisions if the cost of capital < the crossover rate.
- Two projects are of equal size and have the same life.
- Two projects are of equal size but differ in lives.
- As long as the cost of capital (k) is larger than the crossover rate, the two methods both lead to the same decision;
- A conflict exists if k is less than the crossover rate.
- When project size (or scale) differences exist. The cost of one project is larger than that of the other.
- When timing differences exist. The timing of cash flows from the two projects differs in that most of the cash flows from one project come in the early years while most of the cash flows from the other project come in the later years.
- Conventional cash flows means that the initial cash outflows are followed by a series of cash inflows.
- Non-conventional cash flows means that a project calls for a larger cash outflow either sometime during or at the end of its life. Thus, the signs of the net cash flows flip-flop during the project's life.
Some key benefits:
ROIC's limitations:
NPV Profile
This section is not required.
A NPV profile is a graph showing the relationship between a project's NPV and the firm's cost of capital. The point where a project's net present value profile crosses the horizontal axis indicates a project's internal rate of return.
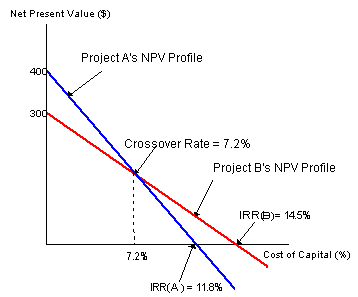
Some observations:
Comparison of the NPV and IRR Methods
The IRR formula is simply the NPV formula solved for the particular rate that sets the NPV to 0. The same equation is used for both methods.
The NPV method assumes that cash flows will be reinvested at the firm's cost of capital, while the IRR method assumes reinvestment at the project's IRR. Reinvestment at the cost of capital is a better assumption in that it is closer to reality.
For independent projects, the NPV and IRR methods indicate the same accept or reject decisions. Assuming that Project A and B are independent, consider their NPV profiles.
However, for mutually exclusive projects, ranking conflicts can arise. Assuming that Project A and B are mutually exclusive, consider their NPV profiles.
For mutually exclusive projects, the NPV and MIRR methods will lead to the same accept or reject decision when:
However, the projects can generate conflicting results if the NPV profiles of two projects cross (and there is a crossover rate):
Two conditions cause the NPV profiles to cross:
The root cause of the conflict between NPV and IRR is the rate of return at which differential cash flows can be reinvested. Both the NPV and IRR methods assume that the firm will reinvest all early cash flows. The NPV method implicitly assumes that early cash flows can be reinvested at the cost of capital. The IRR method assumes that the firm can reinvest at the IRR.
Whenever a conflict exists, the NPV method should be used. It can be demonstrated that the better assumption is the cost of capital for the reinvestment rate (Hint: don't focus too much on this topic, as it is beyond the scope of the CFA exam).
Multiple IRRs is a situation where a project has two or more IRRs. This problem is caused by the non-conventional cash flows of a project.
In fact, non-conventional cash flows can cause other problems, such as negative IRR or an IRR that leads to an incorrect accept or reject decision. However, a project can have only one NPV, regardless of its cash flow patterns, so the NPV method is preferable when evaluating projects with non-normal cash flows.
Corporate Usage of Capital Allocation Methods
The usefulness of various capital budgeting methods depends on their specific applications. Although financial textbooks often recommend the use of NPV and IRR methods, other methods are also heavily used by corporations.
Capital budgeting is also relevant to external analysts in estimating the value of stock prices. Theoretically, if a company invests in positive NPV projects, the wealth of its shareholders should increase.
The integrity of a firm's capital budgeting processes can also be used to show how the management pursues its goal of shareholder wealth maximization.
User Contributed Comments 0
You need to log in first to add your comment.

I passed! I did not get a chance to tell you before the exam - but your site was excellent. I will definitely take it next year for Level II.

Tamara Schultz
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add