- CFA Exams
- 2026 Level I
- Topic 6. Fixed Income
- Learning Module 13. Curve-Based and Empirical Fixed-Income Risk Measures
- Subject 1. Curve-Based Interest Rate Risk Measures
Why should I choose AnalystNotes?
Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.
Subject 1. Curve-Based Interest Rate Risk Measures PDF Download
Callable Bonds
A callable bond exhibits positive convexity at high yield levels and negative convexity at low yield levels. Negative convexity means that for a large change in interest rates, the amount of the price appreciation is less than the amount of the price depreciation.
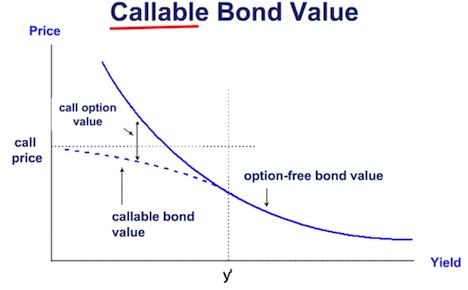
When the required yield for the callable bond is higher than its coupon rate, the bond is unlikely to be called. Therefore, the callable bond will have a similar price/yield relationship (positive convexity) as a comparable option-free bond.
When the required yield becomes lower than the coupon rate, the value of the call option increases because it is getting more and more likely that the bond may be retired at the call price. The call price will set an upper limit on the price of the callable bond. In contrast, for an option-free bond, the bond price will rise unabated as the yield falls. If the required yield rises (but not higher than the coupon rate), the price of the non-callable bond falls and the price of the call option falls. As the price of a callable bond is the difference between the price of the non-callable bond and the price of the embedded option, the price of a callable bond will not fall as much as a non-callable bond. Therefore, a callable bond exhibits negative convexity at low yield levels.
Putable Bonds
The difference between the value of a putable bond and the value of an otherwise comparable option-free bond is the value of the embedded put option.
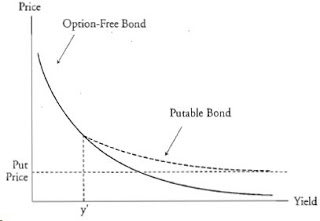
When the required yield for the putable bond is low relative to the issuer's coupon rate, the price of the putable bond is basically the same as the price of the option-free bond because the value of the put option is small. An investor will not sell the bond to the issuer at the put price. Therefore, the putable bond will have a similar price/yield relationship to a comparable option-free bond.
As rates rise, the price of the putable bond declines, but the price decline is less than that for an option-free bond. The value of the put option increases because it's getting more and more likely that the investor will sell the bond to the issuer at the put price. Therefore, the put price sets a lower limit on the price of the putable bond.
Effective duration and effective convexity describe the interest rate risk of bonds with embedded options.
Effective Duration
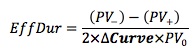
Although they appear similar, the approximate Modified Duration and Effective Duration are different. The Modified Duration is a yield duration statistic that measures interest rate risk with reference to a change in the yield-to-maturity (ΔYield) of the bond. On the other hand, effective duration is a curve duration statistic that measures interest rate risk in terms of a parallel shift in the benchmark yield curve (ΔCurve).
Effective Duration is the best duration measure of interest rate risk when valuing bonds with embedded options because such bonds do not have well-defined internal rates of return (yield-to-maturity). Therefore, yield durations statistics such as Modified and Macaulay Durations do not apply.
Effective Convexity
Effective convexity includes the effects of yield changes on the cash flows. Effective convexity requires an adjustment in the estimated bond values (V-, V+) to reflect any change in estimated cash flows due to the presence of embedded options.
When bonds include embedded options, effective convexity may even be negative. This is in fact just what investors need if they are constructing an estimate that falls within a region of positive convexity, as may be the case with callable bonds.
- When the call option is out of money, the callable bond has positive convexity.
- When the call option is near the money, the effective convexity becomes negative. This is because the callable bond is capped by the price of the call option.
- Putable bonds always have positive convexity.
Since these measures are "effective" they must recognize that a shift in interest rates may bring about a change in cash flows, because embedded options may be exercised. In contrast, modified duration and convexity do not allow for the fact that the cash flows for a bond with an embedded option may change due to the exercise of the option.
In order to calculate effective duration and convexity, we use the binomial model to find both V -and V+. An important assumption is that OAS stays constant when interest rates shift.
A pricing model can be used to estimate the price change resulting from a change in the benchmark yield curve instead of the bond's own yield-to-maturity. V- and V+ are adjusted to reflect any changes in the cash flows (due to embedded options) that result from the change in benchmark yield curve.
User Contributed Comments 6
| User | Comment |
|---|---|
| shiva5555 | Of course, it's so obvious. |
| johntan1979 | The point where a callable bond's curve changes from convex to concave (negative convex) is when coupon rate = required yield |
| Amrokken | Shiva5555 it can be obvious for you and not for others, thanks Jonathan 1979 for clarifying. |
| GBolt93 | Are putable bonds very rare in actual practice? I've heard of callable bonds fairly frequently in school and generally, but this is my first time ever coming across putable bonds. |
| ashish100 | shiva if its so obvious, why are you here? just go take the exam without studying you pothead |
| khalifa92 | differentiate Stocks: called when prices go up to protect the issuer put when prices go down to protect the holder Bonds: called when market yield is lower to refinance at a lower rate. put when market yield is higher to re-invest at higher rates. |

You have a wonderful website and definitely should take some credit for your members' outstanding grades.

Colin Sampaleanu
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add