- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 10. Simple Linear Regression
- Subject 1. Estimation of the Simple Linear Regression Model
Why should I choose AnalystNotes?
Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.
Subject 1. Estimation of the Simple Linear Regression Model PDF Download
Simple Linear Regression
Linear regression is used to quantify the linear relationship between the variable of interest and other variable(s).
The variable being studied is called dependent variable (or response variable). A variable that influences the dependent variable is called an independent variable (or a factor).
For example, you might try to explain small-stock returns (the dependent variable) based on returns to the S&P 500 (the independent variable). Or you might try to explain inflation (the dependent variable) as a function of growth in a country's money supply (the independent variable).
Regression analysis begins with the dependent variable (denoted Y), the variable that you are seeking to explain. The independent variable (denoted X) is the variable you are using to explain changes in the dependent variable. Regression analysis is trying to measure a relationship between these two variables. It tries to measure how much the dependent variable is affected by the independent variable. The regression equation as a whole can be used to determine how related the independent and dependent variables are.
It should be noted that the relationship between the two variables can never be measured with certainty. There always exists other variables that are unknown that may have an effect on the dependent variable.
Estimating the Parameters of a Simple Linear Regression
The following regression equation explains the relationship between the dependent variable and independent variable:
There are two regression coefficients in this equation:
- The Y-intercept is given by b0; this is the value of Y when X = 0. It is the point at which the line cuts through the Y-axis.
- The slope coefficient, b1, measures the amount of change in Y for every one unit increase in X.
Also note the error term, denoted by ei. Linear regression is a technique that finds the best straight-line fit to a set of data. In general, the regression line does not touch all the scatter points, or even many; the error terms represent the differences between the actual value of Y and the regression estimate.
Suppose a regression formula is, yi = -23846 + 0.6942 x xi, where the large constant and the x terms are on a date scale for a spreadsheet program (e.g., Sept 1, 1997 = 35674).
In the regression equation above, the b1 term, 0.6942, represents the slope of the regression line. The slope, of course, represents the ratio of the vertical rise in the line relative to the horizontal "run." The slope and the intercept (b0, here -23846) represent parameters calculated by the regression process. The process of linear regression calculates the parameters as those that minimize the squared deviations of the actual data values from the estimated values obtained using the regression equation. The process of determining these parameters involves calculus.
Linear regression involves finding a straight line that fits the scatter plot best. To determine the slope and intercept of the regression line, one must either use a statistical calculator, a software program, or calculate it by hand. Typically, an analyst will not have to calculate regression coefficients by hand.
- For regression equations with only one independent variable, the estimated slope, b1, will equal the covariance of X and Y divided by the variance of X.
b1 = Cov(X,Y) / (σx)2 = Cov(X,Y)/Var(X) - The intercept parameter, b0, can then be determined by using the average values of X and Y in the regression equation and solving for b0.
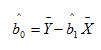
The "hat" above the b terms means that the value is an estimate (in this case, from the regression).
The equation that results from the linear regression is called linear equation, or the regression line.
- Regression line: Y-bari = b0(hat) + b1(hat) Xi
- Regression equation: Yi = b0 + b1Xi + ei, i = 1, 2, ..., n
The linear equation is derived by applying a mathematical method called the least squares regression, also known as the sum of the squared errors: the sum of the squared distances of all the points in the observation away from the mean.
Note that analysts never observe the actual parameter values b0 and b1 in a regression model. Instead they observe only the estimated values b0 and b1. All of their prediction and testing must be based on the estimated values of the parameters rather than their actual values.
After you calculate the b0 and b1, test their significance. Also note that the regression analysis does not prove anything; there could be other unknown variables that affect both X and Y.
User Contributed Comments 7
| User | Comment |
|---|---|
| tabulator | HP12C calculates regression equation coefficients for 1 independent variable. Hallelujah! |
| ybavly | What about the TI BA 2+ anyone know if it has this function and how to use it? |
| Oksanata | what are parameters alfa and beta in normal linear regression assumptions?? is it b0 and b1??? |
| Oksanata | if always keep in mind that error term is differences between actual value of Y (not X) and regression estimate, normal linear regression assumptions no.2,3,4 and 6 become very clear.. |
| luckylucy | To calculate on TI BA 2+ use the data and stat functions. Enter the x and y values in data and stat will give you the results. |
| dysun | Main Content: Linear regression, the meaning of estimated paras, how to get one variable b1 estimation, and other basics. |
| msanderson | Oksanata, would say b1 is the beta and e (error term) represents the alpha as this is the excess return from what is expected by the regression line. |

Your review questions and global ranking system were so helpful.

Lina
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add