- CFA Exams
- 2026 Level II
- Topic 1. Quantitative Methods
- Learning Module 2. Evaluating Regression Model Fit and Interpreting Model Results
- Subject 2. Joint Hypotheses Testing
Why should I choose AnalystNotes?
Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.
Subject 2. Joint Hypotheses Testing PDF Download
Hypothesis tests of a single coefficient in a multiple regression, using t-tests, are identical to those in simple regression. However, testing a hypothesis about β1 and then testing a hypothesis about β2 is not the same as performing a joint test about β1 and β2 simultaneously. To test whether our model explains a significant portion of the variation in Y, we need to perform a joint test of the regression coefficients. In the general regression model, we may want to test the null hypothesis
against the alternative hypothesis
Sequentially performing a series of t tests, each at the 5% level of significance, on each of the coefficients β1, β2, ..., βk, is not the same as jointly testing the null hypothesis that all K coefficients are 0. For example, when we perform two separate t tests on the coefficients β1 and β2, each at the 5% level of significance level, the joint level of significance will not be 0.05. If the probability of rejecting β1 = 0 is 0.05, and the probability of rejecting β1 = 0 is also 0.05, the joint probability of rejecting both β1 = 0 and β2 = 0 is less than 0.05 and depends on the correlation between the sample estimators b1 and b2 (if the estimators were independent, the joint probability of rejecting both hypothesis would be 0.05 x 0.05 = 0.025).
The correct method for testing all the coefficients jointly is based on an F statistic, which follows the F distribution. To perform the test, calculate the F statistic:
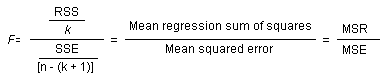
where MSR is the mean regression sum of squares and MSE is the mean squared error.
Continue with the example we have used for previous sections, we want to use a 5% level of significance and test the joint null hypothesis H0: β1 = β2 = 0 against the alternative hypothesis H1: β1 and β2 are not both 0.

From the ANOVA table above, we see that SSE is 20.8958, thus we obtain MSE = 20.8958 / 7 = 2.985.
As RSS is 574.7042, we obtain MSR = 574.7042 / 2 = 287.3521.
Therefore, F = MSR/MSE = 287.3521 / 2.985 = 96.26.
The large value of F indicates that the null hypothesis is false. For α = 0.05, the critical value of F having K = 2 and (n - K - 1) = 7 degrees of freedom is F0.05, 2, 7 = 4.74. We reject H0 in favor of H1 the F statistic of 96.26 far exceeds the critical value.
In fact, the F-statistic can be obtained directly from an ANOVA table (the above is just a part of a complete ANOVA table).
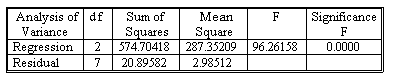
The value "Significance F" represents the prob-value associated with F = 96.26 and is shown to be 0.0000. This provides extremely strong evidence that H0 is false.
The example represents a typical regression model using business data. When we build a model to explain some business data, it's almost always the case that we will reject H0: β1 = β2 = ... = βk = 0 in favor of H1. Rejection of H0 means that, as a group, the explanatory variables do help explain the values of the dependent variable Y, but this result alone does not imply that we have a good model or that the estimated equation will yield good predictions of Y. Nor does it mean that the estimated equation provides a good fit to the data. In general, a good model explains most of the variation in Y and satisfies the statistical assumptions. In practice, most statisticians rely more on R2, se, and the individual t tests than on the overall F test when assessing the quality of some regression model.
The F statistic is related to the value of R2 according to the following equation:
A small value of F strongly indicates that our model is inadequate, but, in general, a small value of F will be accompanied by a small value of R2; consequently, the F-statistic does not provide much additional information about the quality of a model that cannot be learned from inspection of R2 alone.
User Contributed Comments 1
| User | Comment |
|---|---|
| nmech1984 | so whatever we learned so far was BS, because F-statistic does not provide more info than the simple R2. perfect... |

I passed! I did not get a chance to tell you before the exam - but your site was excellent. I will definitely take it next year for Level II.

Tamara Schultz
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add