Why should I choose AnalystNotes?

Simply put: AnalystNotes offers the best value and the best product available to help you pass your exams.

Find out more
Subject 2. Macaulay Duration PDF Download

Bond duration measures the sensitivity of the full price change to a change in interest rates.

  • Yield duration statistics measure the sensitivity of a bond's full price to the bond's own yield-to-maturity. They include the Macaulay duration, modified duration, money duration, and price value of a basis point.

  • Curve duration statistics measure the sensitivity of a bond's full price to the benchmark yield curve, e.g., effective duration.

Duration is the weighted average time to receive the present value of each of the bond's coupon and principal payments. For example, a bond with a duration of three means that, on average, it takes three years to receive the present value of the bond's cash flows.

Macaulay Duration

Frederick Macaulay developed the concept of duration approximately 80 years ago. He demonstrated that a bond's duration was a more appropriate measure of time characteristics than the term to maturity of the bond, because duration incorporates both the repayment of capital at maturity, the size of the coupon and timing of the payments.

Macaulay duration is defined as the weighted average time to full recovery of principal and interest payments. The weights are the shares of the full price corresponding to each coupon and principal payment.

Alternatively, Macaulay duration can be calculated using a closed-form formula.

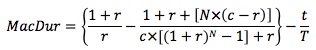
When the investment horizon is greater (less than, equal to) a bond's Macaulay duration, coupon reinvestment risk is higher than (lower than, equal to) the bond's price risk.

Investment Horizon, Macaulay Duration, and Interest Rate Risk

The investment horizon is essential in measuring the interest rate risk of a fixed-rate bond.

When there is a parallel shift to the yield curve, the yield-to-maturity and coupon reinvestment rates are assumed to change by the same amount in the same direction. The Macaulay duration statistic identifies investment horizon so that the losses (or gains) from coupon reinvestment offset the gains (or losses) from market price changes.

The duration gap is the difference between the Macaulay duration and the investment horizon.

  • When the investment horizon is greater than the Macaulay duration of the bond, coupon reinvestment risk dominates price risk. The investor's risk is to lower interest rates. The duration gap is negative.

  • When the investment horizon is equal to the Macaulay duration of the bond, coupon reinvestment risk offsets price risk. The investor is hedged against interest rate risk. The duration gap is zero.

  • When the investment horizon is less than the Macaulay duration of the bond, price risk dominates coupon reinvestment risk. The investor's risk is to higher interest rates. The duration gap is positive.

User Contributed Comments 7

User Comment
kevin from schweser: For coupon paying bonds, duration is less than maturity. Duration is approximately equal to the point in years where the investor receives half of the present value of the bond's cash flows. Since zero-coupon bonds only have one cash flow at maturity, the duration is approximately equal to maturity. Any coupon amount will shorten duration because some cash flow is received prior to maturity.

I am confused. As far as I know, duration is a measure of the price sensitivity of a bond to a change in yield. But maturity is a time unit. How can we connect them together?

Any answer is greatly appreciated.
lawrence The longer the duration the more price sensitive the bond is. A change in interest rate affect distant cashflows more than present cashflows. There are also different measures of duration with different meaning.
Jimish hey
see coupon paying bond are less sensitive because the cash flows are delated..
cuase when cash flows are delayed.. the appropriate discount rate also increases.. its the simple time... discount factor.. so as the zero coupon bond delays all the coupon till maturity... it has a greater duration..
as duration measures the interest sensitivity...... the most sensitive would be the one whose payment are deferred the most...
i hope u got it now
freyalam kevin,
There is an advice that we ignore the unit (usually stated in years) and we need to interpret it as: A duration of x years = for 1% change in YTM, the bond's value will change approximately x %

"approximately" because we are assuming the effective duration as a linear function between the yield rate and bond's value while it is convex.
johntan1979 For those who are using Schweser and don't trust AnalystNotes, please direct your questions to Schweser, since you paid a hefty price for it. While AnalystNotes may not be perfect, many of us are here for the same reasons... value for money, and more comprehensive coverage of the CFA curriculum.
jmorris Jimish is correct. If we recall from the previous reading (was one of the basic bond valuation concepts), i sensitivity is greater on issues with long time horizons. These issues have an inherent discount built in to their PV.
fobucina Duration Gap = Mac Dur - Investment Horizon --> determines which risk (price or reinvestment) dominates
You need to log in first to add your comment.
I am happy to say that I passed! Your study notes certainly helped prepare me for what was the most difficult exam I had ever taken.
Andrea Schildbach

Andrea Schildbach

My Own Flashcard

No flashcard found. Add a private flashcard for the subject.

Add

Actions