- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 3. Statistical Measures of Asset Returns
- Subject 2. Measures of Dispersion
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 2. Measures of Dispersion PDF Download
Dispersion is defined as "variability around the central tendency." Investment is all about reward versus variability (risk). A central tendency is a measure of the reward of an investment and dispersion is a measure of investment risk.
There are two types of dispersions:
- Absolute dispersion is the amount of variability without comparison to any benchmark. Measures of absolute dispersion include range, mean absolute deviation, variance, and standard deviation.
- Relative dispersion is the amount of variability in comparison to a benchmark. Measures of relative dispersion include the coefficient of variance.
The Range
The range is the simplest measure of spread or dispersion. It is equal to the difference between the largest and the smallest values. The range can be a useful measure of spread because it is so easily understood.
The range is very sensitive to extreme scores because it is based on only two values. It also cannot reveal the shape of the distribution. The range should almost never be used as the only measure of spread, but it can be informative if used as a supplement to other measures of spread, such as the standard deviation or semi-interquartile range.
Example: The range of the numbers 1, 2, 4, 6,12,15,19, 26 = 26 - 1 = 25
The Mean Absolute Deviation
The deviation from the arithmetic mean is the distance between the mean and an observation in the data set. The mean absolute deviation (MAD) is the arithmetic average of the absolute deviations around the mean.
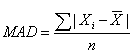
In calculating the MAD, we ignore the signs of deviations around the mean. Remember that the sum of all the deviations from the mean is equal to zero. To get around this zeroing-out problem, the mean deviation uses the absolute values of each deviation.
MAD is superior to the range as a measure of dispersion because it uses all the observations in the sample. However, the absolute value is difficult to work with mathematically.
Sample Variance and Sample Standard Deviation
The variance is a measure of how spread out a distribution is. It is computed as the average squared deviation of each number from its mean. The formula for the variance in a population is:
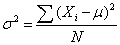
where:
- μ = the mean
- N = the number of scores
To compute variance in a sample:
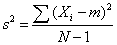
This gives an unbiased estimate of σ2. Since samples are usually used to estimate parameters, s2 is the most commonly used measure of variance.
Note for the sample variance, we divide by the sample size minus 1, or N - 1. In the math of statistics, using only N in the denominator when using a sample to represent its population will result in underestimating the population variance, especially for small sample sizes. This systematic understatement causes the sample variance to be a biased estimator of the population variance. By using (N - 1) instead of N in the denominator, we compensate for this underestimation. Thus, using N - 1, the sample variance (s2) will be an unbiased estimator of the population variance (σ2).
The major problem with using the variance is the difficulty interpreting it. Why? The variance, unlike the mean, is in terms of units squared. How does one interpret squared percentages or squared dollars?
The solution to this problem is to use the standard deviation. The formula for the standard deviation is very simple: it is the square root of the variance. This is the most commonly used measure of spread.
The variance and the standard deviation are measures of the average deviation from the mean.
An important attribute of the standard deviation as a measure of spread is that if the mean and standard deviation of a normal distribution are known, it is possible to compute the percentile rank associated with any given score. In a normal distribution, about 68% of the scores are within one standard deviation of the mean and about 95% of the scores are within two standards deviations of the mean.
Dispersion and Means
The more disperse the returns, the larger the gap between the two means.
Downside Deviation and Coefficient of Variation
Downside risk measures include target deviation, short-fall probability (covered in a different module), and value at risk. A target return must be defined first.
Target Semi-Deviation
Downside risk assumes security distributions are non-normal and non-symmetrical. This is in contrast to what the capital asset pricing model (CAPM) assumes: that security distributions are symmetrical, and thus that downside and upside betas for an asset are the same.
Downside deviation is a modification of the standard deviation such that only variation below a minimum acceptable return is considered. It is a method of measuring the below-mean fluctuations in the returns on investment.
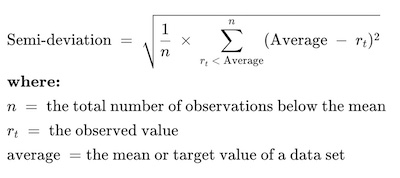
The minimum acceptable return can be chosen to match specific investment objectives.
Semi-deviation will reveal the worst-case performance to be expected from a risky investment.
The semivariance is not used in bond portfolio management extensively because of "ambiguity, poor statistical understanding, and difficulty of forecasting".
Coefficient of Variation
A direct comparison of two or more measures of dispersion may be difficult. For example, the difference between the dispersion for monthly returns on T-bills and the dispersion for a portfolio of small stocks is not meaningful because the means of the distributions are far apart. In order to make a meaningful comparison, we need a relative measure, to standardize the measures of absolute dispersion.
It is often useful to compare the relative variation in data sets that have different means and standard deviations, or that are measured in different units. Relative dispersion is the amount of variability present in comparison to a reference point or benchmark. The coefficient of variation (CV) is used to standardize the measure of absolute dispersion. It is defined as:
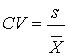
It gives a measure of risk per unit of return, and an idea of the magnitude of variation in percentage terms. It allows us direct comparison of dispersion across data sets. The lower the CV, the better; investments with low CV numbers offer less risk per unit of return. This measurement is also called relative standard deviation (RSD).
Note that because s and X-bar have the same units associated with them, the units effectively cancel each other out, leaving a unitless measure which allows for direct comparison of dispersions, regardless of the means of the data sets.
The CV is not an ideal measure of dispersion. What if the expected return is zero!? Generally, the standard deviation is the measure of choice for overall risk (and beta for individual assets).
Example The mean monthly return on T-bills is 0.25% with a standard deviation of 0.36%. For the S&P 500, the mean is 1.09% with a standard deviation of 7.30%. Calculate the coefficient of variation for T-bills and the S&P 500 and interpret your results.
T-bills: CV = 0.36/0.25 = 1.44
S&P 500: CV = 7.30/1.09 = 6.70
Interpretation: There is less dispersion relative to the mean in the distribution of monthly T-bill returns when compared to the distribution of monthly returns for the S&P 500 (1.44 < 6.70).
User Contributed Comments 9
| User | Comment |
|---|---|
| achu | RSD (rel std dev) = CV. |
| Gooner7 | What does variance even tell you? |
| alester83 | think of variance as vary. it speaks to the likelihood of experiencing returns that are different that average. that is the most simplistic way of looking at it, but to interpret you really need the standard deviation. hope that provides some level of insight |
| LoveIvie | Good overview |
| chipster | what is beta? |
| sgossett86 | hope you're kidding. beta is the first thing you learn in finance class. if you aren't familiar why would you be interested in the cfa. the scarier thing is that you'd be relying on someone to answer this in the thread instead of taking it upon yourself to research. keep checking back. someone will answer it eventually. |
| sgossett86 | without referencing anything, basically beta is a correlation coefficient to a security relative to a major index like the s&p or dow. it's supplied for you from a multitude of online financial sources, and is used in many valuation calculations. it is derived using a regression analysis of returns correlated with the index returns to get ur correlation coefficient |
| sgossett86 | in theory there are leverage calculating formulas, basically finance sourcing, that can solve for a beta without regression |
| fobucina | Beta - essentially, measures the sensitivity of the stock's returns to that of the market portfolio (i.e., we use a major index to proxy for this theoretical portfolio). The levered beta (i.e., the beta incorporating the capital structure of the firm) can be derived using regression analysis... As you will see later on in the curriculum, there are formulas that take the leverage of the firm (D/E), marginal tax rate, and levered beta to determine the firm's unlevered beta (i.e., the beta reflecting the firm's operating risk)... |

I was very pleased with your notes and question bank. I especially like the mock exams because it helped to pull everything together.

Martin Rockenfeldt
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add