- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 3. Statistical Measures of Asset Returns
- Subject 3. Measures of Shape of a Distribution
Seeing is believing!
Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.
Subject 3. Measures of Shape of a Distribution PDF Download
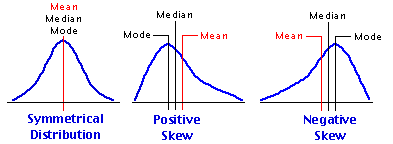
If a distribution is symmetrical, each side of the distribution is a mirror image of the other. For a symmetrical, bell-shaped distribution (known as the normal distribution), the mean, median, and mode of the distribution are equal. The normal distribution can be completely described by its mean and variance.
A distribution is skewed if one of its tails is longer than the other (that is, it is not symmetrical). A symmetrical distribution has no skewness, (the skewness is zero). Skewness refers to the degree of asymmetry of a distribution. It occurs due to the existence of extremely large or small values in the data set. It allows us to see if large positive or negative deviations dominate.
A positively skewed distribution means that it has a long tail in the positive direction (a long right tail). It is sometimes called "skewed to the right." This type of distribution is characterized by many small losses and a few extreme gains.
For a positively skewed distribution, the mode is less than the median, which is less than the mean.
Recall that the mean is affected by outliers. In a positively skewed distribution, there are large positive outliers which will tend to "pull" the mean upward. An example of a positively skewed distribution is that of housing prices. Suppose that you live in a neighborhood with 100 homes. Ninety-nine of those homes sell for $600,000 and there is one house that sells for $3,000,000. The median and the mode will be $600,000, but the mean will be $1,300,000. The mean has been "pulled" upward by the existence of one distinctive home in the neighborhood.
A negatively skewed distribution has a long tail in the negative direction (a long left tail). It is sometimes called "skewed to the left." It is characterized by many small gains and a few extreme losses.
For the negatively skewed distribution, the mean is less than the median, which is less than the mode. In this case, there are large negative outliers which tend to "pull" the mean downward.
Distributions with positive skew are more common than distributions with negative skew. One example is the distribution of income. Most people make under $60,000 a year, but some make quite a bit more, with a small number making many millions of dollars per year. The positive tail therefore extends out quite a long way, whereas the negative tail stops at zero.
In a more psychological example, a distribution with a positive skew typically results if the time it takes to make a response is measured. The longest response times are usually much longer than typical response times, whereas the shortest response times are seldom much less than typical response times.
Negatively skewed distributions do occur, however.
Tips on how to remember these relative locations:
- The mean is always in the direction of the skew. For example, a positively (negatively) skewed distribution skews to the right (left), so its mean is on the right (left). This is because the mean is unduly influenced by extreme values.
- The median is always in the middle.
a typical exam question: There is a certain probability distribution with the characteristics described below:
- Mean = 100
- Highest possible value = 200
- Lowest possible value = 20
What type of distribution is this?
When a distribution is normal, the dispersion to the left of the mean is the same as the dispersion to the right of the mean. The highest number above (200) is 100 units larger than the mean, whereas the lowest number (20) is 80 units below the mean. Thus, the distribution is not symmetrical. It is skewed to the right.
We've just discussed skewness, which refers to the deviation from a normal distribution due to asymmetry. A distribution may deviate from the normal distribution by being more or less peaked than a normal distribution.
Kurtosis
Kurtosis is based on the size of a distribution's tails. It is the statistical measure that tells us when a distribution is more or less peaked than a normal distribution.
- Distributions with small tails (that is, less peaked than normal) are called "platykurtic." If a return distribution has more returns with large deviations from the mean, it is platykurtic.
- Distributions with relatively large tails (that is, more peaked than normal) are called "leptokurtic." If a return distribution has more returns clustered closely around the mean, it is leptokurtic.
- A distribution with the same kurtosis as the normal distribution is called "mesokurtic."
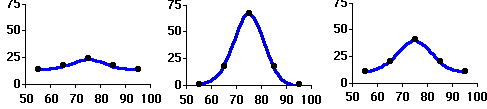
Kurtosis is critical in a risk management setting. Most research on the distribution of securities returns has shown that returns are not normal. Actual securities returns tend to exhibit both skewness and kurtosis (sounds like fungus!). Skewness and kurtosis are critical for risk management because if securities returns are modelled after a normal distribution, predictions from those models will take into consideration the potential for extremely large negative outcomes. In fact, most risk managers put very little emphasis on the mean and standard deviations of a distribution and focus more on the distribution of returns in the tails of the distribution, since this is where the risk is.
To calculate skewness (when N is large):
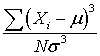
where μ is the mean and σ is the standard deviation.
The normal distribution has a skew of 0, since it is a symmetric distribution.
If skewness is positive, the average magnitude of positive deviations is larger than the average magnitude of negative deviations.
To calculate excess kurtosis (when N is large):
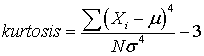
The kurtosis equals excess kurtosis + 3.
For all normal distributions, kurtosis is equal to 3; excess kurtosis is equal to 0.
A leptokurtic distribution has an excess kurtosis greater than 0, and a platykurtic distribution has an excess kurtosis less than 0.
User Contributed Comments 43
| User | Comment |
|---|---|
| chandos | PLATY, LEPTO, MESO |
| cwrolfe | NINA, PINTA, SANTA MARIA |
| vadimmuchnik | Pasha, Liesha, Misha |
| AusPhD | alpha, beta, gamma |
| achu | "lepto" leaps OVER normal kurtosis. platy is thus under the normal kurtosis. kurtosis = formula "+0" The -3 constant is added to calcluate XS kurtosis. |
| GeorgeC | Remember "platy" is like "plateau" which is flat - thus the platykurtic distribution is flatter. |
| mordja | Veni, Vidi, Vici |
| TammTamm | Uno, Dos, Tres |
| ravdo | ep, dog, dig. |
| hedgefrog | typical exam question: i'm not sure it's correct. Take sample: 20, 60, 110, 110, 200. Mean=100. Median=mode=110. Negative skew. another sample: 20 90 90 200. mean=100. median=mode=90. positive skew. |
| alyl21 | Distributions with small tails (that is, less peaked than normal) are called "platykurtic." If a return distribution has more returns with large deviations from the mean (and thus has fatter tails), it is platykurtic. Note the error in GeorgeC's comment: Platykurtic is less peaked and has thinner tails, not fatter tails. Check CFA curriculum |
| Criticull | I second alyl21's comment since the distribution is less peaked, but still must have total probability sum to one between the pdf and the horizontal axis. |
| TonLoc | hedgefrog, your math is wrong |
| jack1jack | I agree with alyl21. leptokurtic return distribution is has the fatter tail. |
| anastasiya | The formulas posted here are valid only if N gets large - both for the skewness and the kurtosis. The CFA textbook gives broader and more complex formulas but there's no way to memorize them. |
| ccharles | Trick to remember: Put the words Mean, Median and Mode in alphabetical order If Mean < Median < Mode, < points to the left so it is left / negatively skewed. If Mean > Median > Mode, > points to the right so it is right / positively skewed. |
| rhardin | Hedgefrog's math is right. |
| rhardin | Way to remember: Leptokurtic needs liposuction because it's tails are fat! |
| tschorsch | you cannot assume from a single simple 5 value example that this is the way it works with larger distributions. with a skewed to the right distribution approximately normal distribution, usually, max-mean > mean-min. you have a tail with a very small percentage of the values still pulling the mean in the direction of the tail. but the outliers in the tail can be far greater than the opposite outliers. if you even look at the 5 value sample, there are two lower outliers, 20 and a marginal outlier 60 where you have only one upper outlier. with a small sample size, you can usually create something odd that does not correspond with data sets of significant size that are more bell shaped. |
| AUAU | Normal Distribtn : mean = median = mode ; skewness = 0; symmetric; discribed by mean & variance. +ve skewness: mod<med<mean [+ve(right) tail] |
| ciji | A platykurtic distribution is like a platypus |
| thekid | Can someone please explain.... How the 'mode' is equal to the mean and median in a normal distribution? Thanks. |
| Gooner7 | @thekid dont worry about all that. Think about it as follows: On a test, the median score was 70%, but the average was 65%. That indicates that the distribution was to the negative, negative skew. |
| jpducros | These definitions seems basic but need special attention since it is quite easy (for me at least) to make a mistake. Confusion is even more probable when you'll work on t-distribution and degree of freedom. The higher the df, the higher the peak, but the thinner the tails (different from what we've seen above). In other words, don't confuse degree of freedom and lepto/platy kurdic. Hope it helps. |
| Kbrooks80 | An electron is a lepton. For leptokurtic just think of the mean as a conductive wire running vertically through the distribution that the electrons gravitate toward. |
| hiyujie | Ccharles, good summary |
| moon13 | Thanks Ccharles!! |
| dipu617 | ek, dui, tin ..... |
| rockstarchuckie | een, twee, drie |
| Creep | apple, cat, schizophrenic |
| bidisha | yea good tip ccharles |
| chipster | Have to say the explanation here of the whole concept was superior to that in the CFA reference material!! Good work AN. |
| RamaG | lepto = normality takes a leap playto = normality is played down |
| schweitzdm | Notice that the LOS does not say that we need to know to calculate kurtosis. Need to be able to explain though. |
| sahilb7 | L for Lepto - L for Long P for Platy - P for Plateau M for Meso - M for Middle |
| ravinram | For further information on this topic, pls visit the website: vassarstats.net/textbook/ch2pt1.html |
| cfastudypl | Thanks AN for the simplification of the concepts! |
| forry9er | PLATYKURTIC distributions have FLAT tails like a PLATYPUS. Didn't anyone take Latin? |
| ashish100 | these guys are losing their mind studying for this |
| khalifa92 | you'ven't seen anything yet. |
| fin_guy | I don't get it. They say kurtosis is "peaky" or "flatty" of returns. Then there is "kurtosis risk". Why is "peaky" or "flatty" called "risky"? |
| tejerius | pim, pam , pum, bocadillo de atún |
| ocanas | XBOX, NINTENDO, SONY |

Your review questions and global ranking system were so helpful.

Lina
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add