Seeing is believing!

Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.

Find out more
Subject 2. Par and Forward Rates PDF Download

A forward rate refers to the interest rate on a loan beginning some time in the future. In contrast, a spot rate is the interest rate on a loan beginning immediately. For example, the two-year forward rate one year from now is 4%. This means that if you borrow a two-year loan one year from now, you will pay an interest of 4%.

A forward curve is a series of forward rates, each with the same time frame.

Forward rate calculations are usually based on a theoretical spot rate curve. They are sometimes referred to as implicit forward rates.

Given spot rates for maturities of j and k years, you can compute the forward rate (fj, k-j) that applies for the period from year j to year k using the relationship:

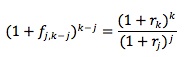
Example

Compute the annualized six-month forward rate two years from now.

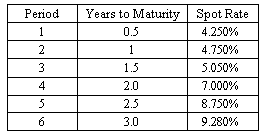
In order to compute the six-month forward rate two years from now, first determine the spot rate for the fifth period (0.087) and the spot rate for the fourth period (0.0700). Then complete the following calculation: [(1 + 0.0875/2)5/(1 + 0.0700/2)4] - 1 = 7.95%.

Similarly, implied spot rates can be calculated as geometric average of forward rates.

Interpreting their Relationship

We can make the following observations:

  1. The spot rates are positive, and the spot curve is upward sloping.

  2. The spot and par curves are nearly identical; the par rates are slightly lower than the spot rates, and the slight difference between the spot and par curves is greater at longer maturities.

  3. Forward rates are greater than the spot and par rates.

User Contributed Comments 15

User Comment
kalps THIS IS RUBBISH AND WORRYING AS YOU DIVIDE THE SPOT RATES BY TWO BUT THEY KEEP THE POWERS THE SAME - SURELY THEY SHOULD BE DOUBLED TO REFLECT THE FACT THAT YOU ARE LOOK AT SEMI ANNUAL PERIODS - CAN SOMEONE CONFIRM THIS IS TRUE IT WHETHER I AM TALKING RUBBISH ??
shasha sorry kalps, i believe you got some concepts wrong here. 1st, spot rates are always annually quoted. 2ndly, when you see "1f14" referring to six month forward rate (of course 14 periods from now), you'd understand "one period" is six months, and 14 periods is 7 years. when "1f14" is calculated, all calculation must be based on six-month interval, so spot rate is divided by 2, as per the powers, they're already "doubled", say, from 7 (years) to 14 (intervals), so powers are kept unchanged. re the mistake, the answer did got one: question is asking for 1f14, it should be 7.72%. Should annualized rate be asked, the answer would be 15.44% then.
theLogic Shasha: the answer is correct: it has the same numbers as you indicate. So what's wrong with it?
kkevin77 Does anybody have a quick and dirty answer to construct the forward yield curve? I'm trying to calculate the 10-yr treasury two years from now?
Treynor I don't know what maturities that are available for Treasuries (since I am not living in US) but the calculation is pretty straightforward.

today's yield on 2-year^2 * future(2years from now) 10-year^10 = today's 12-year^12

You have the 2-year yield and if you don't have any 12-year you will have to approximate this one. For example through interpolation between a 10 year and a longer bond. After that you simply solve for the forward 10-year yield.
synner all forward rates are reported in annual rates just like spot rates. so need to multiply it by 2 to get the final answers. 15.446% is correct.
NillePet The assumption when calculating forwrad rates is that there are no abitrage possibilties. Thus, investing $100 for 15 periods must have the same return as investing $100 for 14 periods + reinvest the outcoming for another period.

Here we have a return for 15 periods of:
100 * (1+0.056139/2)^15 = 151,54

The return for 14 periods is:
100 * (1+0.04929/2)^14 = 140,52

Thus the forward rate 1f14 is:
(151,40-140,52)/140,52 = 7,84 %

This is equal to: (1+0.056139/2)^15/(1+0.04929/2)^14

So, I believe that 15,446% is wrong. If you search on google for forward rate calculations / definitions you find my caculation confirmed.
(1+0.056139/2)^15/(1+0.04929/2)^14
zackychoo Is the convention of converting semi-annual to annual rates assumed in the exam? That is, do we definitely multiply or divide by 2 instead of squaring and rooting?
SeanDec10 NillePet - you did not carry enough decimal places in your calculation and are suffering from round-off error.
johntan1979 Sounds like kalps is referring to himself
floydbite hey in the first example how did they get i=2.6609%??? I got i=4.1339% directly. And do we have to annualize i (*2) or just i is directly the answer?
vfabianv Hello floybide, how did you get the i=4.1339% directly?
BIDA11 Is there a way to quickly calculate this on the BA II Plus calculator? Also how did you derive the interest of 102.055/(1+i/2)4 , i = 2.0669%, i cant seem to get my head around this. Thanks
amingraham Calculate
FV = 102.055
PV = 100 - 2.0246 - 1.9888 - 1.9506 = 94.036
PMT = 0
N = 4
CPT I/Y = 2.0669
phill amingraham, how did you get 102.055 for FV? Also, in the answer, they use 2.055 as the PMT, where does that come from? Thanks!
You need to log in first to add your comment.
Your review questions and global ranking system were so helpful.
Lina

Lina

My Own Flashcard

No flashcard found. Add a private flashcard for the subject.

Add

Actions