Seeing is believing!

Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.

Find out more
Subject 1. Periodicity and Annualized Yields PDF Download

Fixed-rate bonds are those that pay the same amount of interest throughout their specified term. Measurement for fixed-rate bonds depends on the timing of the bond's cash flows.

Yield measures are used to evaluate the rate of return on bonds.

  • They are typically annualized.
  • Money market rates are simple interest rates. They are annualized but NOT compounded.
  • Non-money market rates are compounded.

Yields-to-maturity allow analysts to use a single measure to compare bonds with varying maturities and coupons.

The periodicity of an annual interest rate is the number of periods in the year.

Consider a two-year, zero-coupon bond priced now at 88 per 100 of par value.

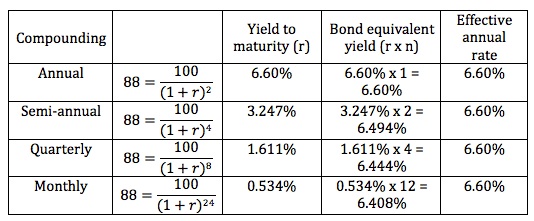
Note:

  • The effective annual rate is the same.
  • The bond equivalent yield and the periodicity are inversely related.
  • When comparing different bonds, it is essential to compare the yields for the same periodicity to make a statement about relative value.

To convert an annual yield from one periodicity to another:

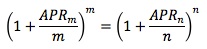
Example

  • A Eurobond pays coupons annually. It has an annual-pay YTM of 8%.
  • A U.S. corporate bond pays coupons semi-annually. It has a bond equivalent YTM of 7.8%.
  • Which bond is more attractive, if all else equal?

Solution 1

  • Convert the U.S. corporate bond's bond equivalent yield to an annual-pay yield.
  • Annual-pay yield = [1 + 0.078/2]2 - 1 = 7.95% < 8%
  • Therefore, the Eurobond is more attractive since it offers a higher annual-pay yield.

Solution 2

  • Convert the Eurobond's annual-pay yield to a bond equivalent yield (BEY).
  • BEY = 2 x [(1 + 0.08)0.5 - 1] = 7.85% > 7.8%
  • Therefore, the Eurobond is more attractive since it offers a higher bond equivalent yield.

User Contributed Comments 12

User Comment
CHADZAMIRA This is reasonably straight forward but be careful with the conversion process.
ramtor use the iconv function of BAII plus
JimM Using the ICONV function of BAII plus (it's on the "2" key), remember to set C/Y = 2, not 365.

NOM = BEY
EFF = Annual-pay yield

Set 1 of those, CPT the other.
jpducros Remember that you'll always have :
MMY<BEY<EAY
MMY : Money Market Yield : no compounding - 360 d/year
BEY : Bond Equiv. Yield : Semi-Annual Compounding - 365 d/y
EAY : Effective annual Yield : compounding for the entire year, based on 365 d/y
anaraguin Thank you so so much JimM! :)
moneyguy That still doesn't tell me how to actually apply the iconv button to calculate this stuff, JimM
2014 thanks jim
tichas Chadzamira , iwe
SAB1987 Thank you JimM
davidbenke @moneyguy
US corporate bond example:
[2nd][2]
NOM = [7][.][8]
C/Y = [2]
EFF = [CPT]

EFF should equal 7.952
philerup TIL how to use ICONV. Thanks Jim!
phill why do them all have the same EAR and how is that calculated?
You need to log in first to add your comment.
I used your notes and passed ... highly recommended!
Lauren

Lauren

My Own Flashcard

No flashcard found. Add a private flashcard for the subject.

Add

Actions