Four ratios are commonly used for this purpose.

Sharpe Ratio

It is a measure of the excess return per unit of risk. It defined as the portfolio's risk premium divided by its risk: 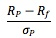. This ratio is easy to use. The two limitations are:

• It uses standard deviation, not beta, as a measure of volatility.
• The ratio itself is not very informative.

Treynor Ratio

It measures the excess return on an investment which has no diversifiable risk. Systematic risk is used instead of total risk: 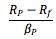. Again, the ratio itself is not very informative, and it cannot be applied to assets with negative βs. It is a ranking criterion which is easy to use.

M-Squared (M²)

It is a performance measurement using return per unit of total risk as measured by the standard deviation. The investment portfolio's standard deviation is adjusted to reflect the standard deviation of the market benchmark portfolio. The return premiums of the adjusted investment portfolio and the market index portfolio are then compared.

Jensen's Alpha

It is the abnormal return over the theoretical expected return. The theoretical expected return is calculated using CAPM (and beta): α _p = R_p - [R_f + β(R_m - R_f)]. Since the CAPM return is supposed to be risk-adjusted, Jensen's α is also risk-adjusted. Investors are constantly seeking investments that have positive α or "abnormal returns."

If an investor holds a portfolio that is not fully diversified, total risk matters. Sharpe ratio and M-squared are appropriate performance measures in such cases. On the other hand, if the portfolio is well-diversified, Treynor ratio and Jensen's alpha are relevant, as only the systematic risk of the portfolio matters.