- CFA Exams
- 2026 Level I
- Topic 1. Quantitative Methods
- Learning Module 1. Rates and Returns
- Subject 2. Rates of Return
Why should I choose AnalystNotes?
AnalystNotes specializes in helping candidates pass. Period.
Subject 2. Rates of Return PDF Download
A financial asset's total return consists of two components: an income yield consisting of cash dividends or interest payments, and a return reflecting the capital gain or loss resulting from changes in the price of the financial asset.
Holding Period Return
It is the percentage by which the value of an investment has grown for a particular period. It is the sum of investment income and capital gains divided by the initial value.
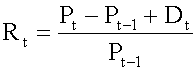
It has two important characteristics:
- It has an element of time attached to it: monthly, quarterly or annual returns. HPR can be computed for any time period.
- It has no currency unit attached to it; the result holds regardless of the currency in which prices are denominated.
Example
A stock is currently worth $60. If you purchased the stock exactly one year ago for $50 and received a $2 dividend over the course of the year, what is your holding period return?
Rt = ($60 - $50 + $2)/$50 = 0.24 or 24%
Arithmetic or Mean Return
The arithmetic mean is what is commonly called the average. It is the most widely used measure of central tendency. When the word "mean" is used without a modifier, it can be assumed to refer to the arithmetic mean. The mean is the sum of all scores divided by the number of scores.
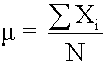
- All interval and ratio data sets (e.g., incomes, ages, rates of return) have an arithmetic mean.
- All data values are considered and included in the arithmetic mean computation.
- A data set has only one arithmetic mean. This indicates that the mean is unique.
- The arithmetic mean is the only measure of central tendency where the sum of the deviations of each value from the mean is always zero. Deviation from the arithmetic mean is the distance between the mean and an observation in the data set.
The arithmetic mean has the following disadvantages:
- The mean can be affected by extremes, that is, unusually large or small values (outliers). In such cases we can either do nothing, or delete all the outliers (trimmed mean), or replace the outliers with another value (winsorized mean).
- The mean cannot be determined for an open-ended data set (i.e., n is unknown).
Geometric Mean Return
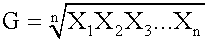
The geometric mean has three important properties:
- It exists only if all the observations are greater than or equal to zero. In other words, it cannot be determined if any value of the data set is zero or negative.
- If values in the data set are all equal, both the arithmetic and geometric means will be equal to that value.
- It is always less than the arithmetic mean if values in the data set are not equal.
It is typically used when calculating returns over multiple periods. It is a better measure of the compound growth rate of an investment. When returns are variable by period, the geometric mean will always be less than the arithmetic mean. The more dispersed the rates of returns, the greater the difference between the two. This measurement is not as highly influenced by extreme values as the arithmetic mean.
The Harmonic Mean
The harmonic mean of n numbers xi (where i = 1, 2, ..., n) is:
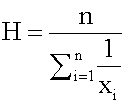
The special cases of n = 2 and n = 3 are given by:
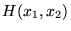
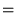
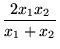
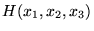
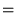
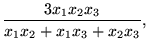
and so on.
For n = 2, the harmonic mean is related to arithmetic mean A and geometric mean G by:
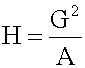
The harmonic mean may be viewed as a special type of weighted mean in which an observation's weight is inversely proportional to its magnitude. It is used most often when the data consists of rates and ratios, such as P/Es.
Which Mean to Use
It depends on lots of factors: outliers, symmetric distribution? compounding?
- Include all values, including outliners? Arithmetic mean.
- Compounding required? Geometric mean.
- Minimize the impact of extreme outliners? Harmonic mean, trimmed mean, winsorized mean.
In general:
Harmonic Mean <= Geometric Mean <= Arithmetic Mean
User Contributed Comments 20
| User | Comment |
|---|---|
| MURF | how do you do a geometric mean with a negative number?? 5, -3, 6 |
| chandos | it cannot be calculated if one of the values is -ve |
| aggieguy05 | it can too be done. (1.05*.97*1.06)=g^3 |
| db28luke | you add 1 to each return and take the nth root minus 1 |
| db28luke | its in the book...page 125 |
| mogulcn | in the case above, it is still positive as the data set are 1+Rt. in the book, it is said that the observations will never be negative becasue the biggest negative return is -100% |
| achu | think of geometric mean as something like "multiplicative mean" average- product of n items then taken to 1/n th power. |
| valerycfa | When calculating variance, why do we loose a degree of freedom when passing from population to sample calculation ? |
| Mariecfa | If the sample variance were defined with division by n, it would systematically underestimate the value of the population variance. So, we compensate by increasing its overall value by making its denominator smaller (by using n-1 instead of n). Division by (n-1) causes the sample variance to target the value of the population variance, whereas division by (n) causes the sample variance to underestimate the value of the population variance. |
| AmyJ | How do you solve for Geometric mean with an HP 12C calculator? Thank you. |
| boddunah | amyJ hp 12c platinum solution for geometric return. for example yearly returns are 5%,(3%),2% geometric return as follows step 1 :1.05*0.97*1.02 = 1.038870. (3% is negative return. so 1-0.03=.97) step 2: enter 3 and press button 1/x .result = 0.3333.(we used 3 bc 3 years returns were given) step 3 :0.3333 (already entered) press button Y^x. It should give you 1.0128. step 4 : subtract 1 from 1.0128 = 0.0128 0r 1.28% geometric return. |
| jpducros | What do we use an harmonic mean for ? |
| knowles242 | as jpducros indicated is there an application of the harmonic mean? |
| Mosobalaje | Harmonic mean is generally used to measure average investment costs over a time period. It's not used to calculate returns. |
| Barchie | Why is it that the geometric mean is not as affected by the extremes? (that is it's advantage, I just don't get why not.) |
| birdperson | 2 other "fun" facts -- sum of deviations from the (arithmetic) mean = 0 -- when the values are positive and not equal, H < G < A |
| Kholofelo | Another way to look at the typical exam question is to say If this were a normal distribution my average would be 100 Using 80 as a spread either way (20 + 180) / 2 = 100 OR using 100 as a spread either way (0 + 100) / 2 = 100 By having 20 has my lower limit and 200 as my upper limit, my average is pulled "upward" or to the right of the mean i.e. (20 + 200) / 2 = 110 hence it is skewed to the right of the mean. |
| Kholofelo | *(0 + 200) / 2 = 100 |
| unknown | the geometric mean of 5 variables can be done (x1*x2*x3*x4*x5)^1/5, because the square root in BAII is standardized for one underlying. |
| RoL9833Y | The curriculum specifies the A.M. x H..M. = (G.M.)^2 but needs not to prove. However, this formula can be one of the questions being construed ! |

I used your notes and passed ... highly recommended!

Lauren
My Own Flashcard
No flashcard found. Add a private flashcard for the subject.
Add