Seeing is believing!

Before you order, simply sign up for a free user account and in seconds you'll be experiencing the best in CFA exam preparation.

Find out more
Subject 2. Arbitrage and Replication PDF Download

Option Arbitrage

As derivative securities, options differ from futures in a very important respect. They represent rights rather than obligations - calls gives you the right to buy and puts gives you the right to sell. Consequently, a key feature of options is that the losses on an option position are limited to what you paid for the option, if you are a buyer. Since there is usually an underlying asset that is traded, you can, as with futures, construct positions that essentially are risk-free by combining options with the underlying asset.

The easiest arbitrage opportunities in the option market exist when options violate simple pricing bounds. The previous discussion tells us that the price is somewhere between zero and maximum, which is either the underlying price, the exercise price, or the present value of the exercise price - a fairly wide range of possibilities. The range will be tightened up a little on the low side by establishing a lower bound on the option price.

For American options, which are exercisable immediately:
C0 >= Max (0, S0 - X)
P0 >= Max (0, X - S0)

For instance, a call option with a strike price of $30 on a stock that is currently trading at $40 should never sell for less than $10. It it did, you could make an immediate profit by buying the call for less than $10 and exercising right away to make $10.

If the option is in-the-money and is selling for less than its intrinsic value, it can be bought and exercised to net an immediate risk-free profit.

In fact, you can further tighten these bounds for call options, if you are willing to create a portfolio of the underlying asset and the option and hold it through the option's expiration. The bounds then become:

  • With a call option: Value of call > Value of Underlying Asset - Present value of Strike Price
  • With a put option: Value of put > Present value of Strike Price - Value of Underlying Asset

Too see why, consider the call option in the previous example. Assume that you have one year to expiration and that the risk-less interest rate is 10%.

Present value of Strike Price = $30/1.10 = $27.27

Lower Bound on call value = $40 - $27.27 = $12.73

The call has to trade for more than $12.73. What would happen if it traded for less, say $12? You would buy the call for $12, sell short a share of stock for $40 and invest the net proceeds of $28 ($40 - 12) at the risk-less rate of 10%. Consider what happens a year from now:

If the stock price > $30: You first collect the proceeds from the risk-less investment ($28(1.10) = $30.80), exercise the option (buy the share at $30) and cover your short sale. You will then get to keep the difference of $0.80.

If the stock price < $30: You collect the proceeds from the risk-less investment ($30.80), but a share in the open market for the prevailing price then (which is less than $30) and keep the difference.

In other words, you invest nothing today and are guaranteed a positive payoff in the future. You could construct a similar example with puts.

The arbitrage bounds work best for non-dividend paying stocks and for options that can be exercised only at expiration (European options). However, European options cannot be exercised early; thus, there is no way for market participants to exercise an option selling for too little with respect to its intrinsic value. Investors have to determine the lower bound of a European call by constructing a portfolio consisting of a long call and risk-free bond and a short position in the underlying asset.

Consider an American call option. First the investor needs the ability to buy and sell a risk-free bond with a face value equal to the exercise price and current value equal to the present value of the exercise price. The investor buys the European call and the risk-free bond and sells short (borrows the asset and sells it) the underlying asset. At expiration the investor shall buy back the asset.

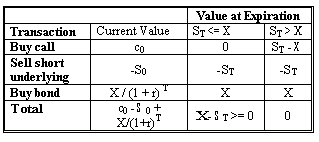
This combination produces a non-negative value at expiration, so its current value must be non-negative. For this situation to occur, the call price has to be worth at least the underlying price minus the present value of the exercise price:

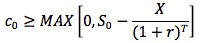
Option Replication

Two assets that provide the same cash flow must logically have the same value/price. This concept is derived from the underlying valuation principle in finance that states that the value of any asset is the sum of the present values of all future cash flows. So if the cash flows of two assets are the same, the price or value must be equal.

The replicating portfolio to value a call option is a long position in the stock with borrowed money. This portfolio is called a replicating portfolio because if you borrowed money and purchased a specific number of shares in the stock, your payoff will exactly match the payoff from the call option.

The replicating portfolio to value a put option is a short position in the stock and purchase of a bond. This portfolio is called a replicating portfolio because if you sold the stock now and lent the present value of the stock, your payoff will exactly match the payoff from the put option.

The number of shares you will buy or sell (short) to create a replicating portfolio will be based on the hedge ratio or option delta.

User Contributed Comments 23

User Comment
6162 the reason behind this is that the buyer can use his part of money for some other investment purposes when the interest rates r high in the market but paying only a margin amount of the option whereas the writer or the seller cannnot sell the goods until the buyer wishes so he is stuck with the stock and cannot convert it into cash and benefit the high rate of interest in the market.
mtcfa Am I the only one that thinks this section is somewhat off base? If I have an equity call that goes in my favor (ie deep in the money), you can bet I'm going to excercise that option and take my profits. Why would I sit around and wait for the market to turn againat me and lose what ever profits I already made?
cwrolfe I'd just short the call option and lock-in my gains
antarctica Here it's assumed that price rises continuously. So if you exercise now you'll be worse off than keeping it until expiration, assuming that stock price either goes up or stay the same.
Winner Euro Call Max I get 9.92 rather than 9.52 as detailed above. Does anyone else get this answer?
Winner Sorry, Now I see how they get the 9.52, its
clearer if you see it like this
50 - [(60/(1.05^.1644)] = -9.52
uberstyle kind of a strong assumption to assume prices continue to rise - I am not disagreeing but wonder why it is not noted?
Tom81 Solution

* Time to expiration (T) = 60/365 = 0.1644.
* European Call (c0): MAX[0, 50 - 60/(1 + 5%)0.1644] = MAX[0, -9.52] = 0.
* American Call (C0): MAX[0, 50 - 60/(1 + 5%)0.1644] = MAX[0, -9.52] = 0.
* European Put (p0): MAX[0, 60/(1 + 5%)0.1644 - 50] = MAX[0, 9.52) = 9.52.
* American Put (P0): MAX[0, 60 - 50) = 10.
* Note that the lower bound of the American put is above the lower bound of the European put.


Should that not just be for an American Max(0,50-60), i.e. not discounted.
olagbami Why is the American call option discounted?
tschorsch You would just sell the option to lock in profits.
It is still worth more than the intrinsic value because the underlying could still go more in your favor.
Also, exercising an option would give exposure to the underlying, and you would also usually incure more transaction costs by exercising.
tschorsch Also, suppose you are long a call. When the underlying price hits your target, you want to exit the position. When you exercise, you are still net long the position and must sell the underlying to remove your exposure. Exercising is not instantaneous and you will have some time exposure when you cannot exit (unless you sell the underlying short).
The moral of the story is, unless you want to hold the underlying for the longer term (or for puts you already have the underlying and want to unload it) it is really not worth exercising just to take profits.
Shammel @ olagbami: I think the American call option is discounted as we are finding the lower bound.
cardinal08 The call is using leverage, "borrowing," to buy the underlying later. The put is holding the premium. In a high interest rate environment, This is beneficial to the call holder because he is achieving leverage without needing to finance through high rates, and this disadvantages the put holder because he is holding a premium that would otherwise be paying a high rate.
Juhee American call can be exercised before expire date not like European call. so that is why we need to discount to get the present value
anova The lower bounds of American and European Calls are the same else the American Call lower bound would be lower the European Call lower bound.
co>= Max[0,So-X/(1+r)^T]
Co>= Max[0,So-X/(1+r)^T]
papajeff They are referring only to exercising the option, not selling the calls. if you sell the call you lock in the time value.
moneyguy At least this stuff is not at all confusing.
Emily1119 Why a long term european put can be worth more or less than a short term european&#65311;
Oksanata in this case they should have discounted American put as well, shouldn't they?
Oksanata Oh, now I see..All the explanations are in No.9 of this subject..
Oksanata If Volatility, Time to Expiration is UP - Call and Put values are UP
All other factors,if UP, affecting option prices in opposite directions as follows:
Dividents, Strike Price UP: Call Down, Put Up
Intr.Rate, Underlying UP: Call UP, Put Down
gill15 Why would it be confusing to you? You're the Moneyguy.
SKIA This section should have a couple of questions to hammer on the relationships.
You need to log in first to add your comment.
I am using your study notes and I know of at least 5 other friends of mine who used it and passed the exam last Dec. Keep up your great work!
Barnes

Barnes

My Own Flashcard

No flashcard found. Add a private flashcard for the subject.

Add

Actions